DSE 2010: Q.32

[n.saish]

Consider an exchange economy with agents 1 and 2 and goods x and y. Agent 1's endowment is (0,1) and agent 2's endowment is (2,0). Suppose agent 1 lexicographically prefers x to y. Suppose agent 2 treats x and y as perfect substitutes.
The set of all competitive equilibrium prices consist of Px>0 and Py>0 such that.
(a) Px/Py   = 1
(b) Px/Py >= 1
(c) Px/Py <= 1
(d) Px/Py > 0

Sir, my doubt is that the answer should be (b) Px/Py >= 1 and not (a) as given in the solutions.
Reasoning: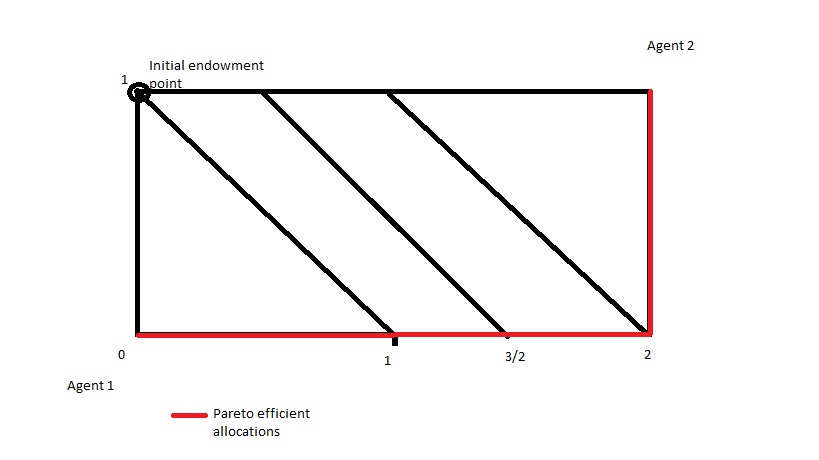



Now if Px< Py then agent 2 will want to consume only good x and his choices will lie on the upper edge of the edgeworth box and will not lie on the pareto efficient allocations.
If Px=Py then he would be indifferent between comsuming the two goods as long as he lies on the same indifference curve, so he would be willing to move his choices onto the red line
If Px>Py then he will want to consume only good y, but as there is only 1 unit of good 2 in the economy he will consume 1 unit of y and then move onto consuming x to move onto a higher indifference curve. All these points also lie on the pareto efficient allocation line (the red line)
Hence the ans should be (B)

An alternative reasoning can be if the economy is moving from (0,1),(2,0) to (1,0),(1,1) then agent 2 would exchange 1 good of y for 1 good of x only if the price of x is equal to y or the price of x is greater than y. So this way to I land up at the same answer.
Could you tell me if there is any flaw in my reasoning?

[aditi5000]

a1's income = p2
a2;s income = 2p1

set p1=1 as numeraire
a2s income = 2

at p1>p2 a2 only consumes good y so y2=2/p2 and x2=0
but a1 lexicographically prefers x to y so x2=p2/p1 and y1=0
adding y1 and y2 = 2/p2 = resource of the economy =1 this gives p2=2 ie a contradiction from our assumption p1>p2

p1<p2 a2 only consumes good x thus x2=2 and y2=0 and for a1, x1=p2 and y2=0 thus excess supply of good y and also, 2+p2=2 gives p2=0 again a contradiction of assumption p1<p2

so p1=p2=1 .. work it out in the same manner you'll get the situation that both markets clear.

[n.saish]

Thanks a lot for replying Aditi, I get what you're saying, but when you're saying that y1+y2 = 2/p2 = 1 and hence p2=2 means what price would good 2 need to have to be, so that consumer2 can consume the entire allocation of y in the economy, but we have a limited allocation of good y. So even if 2/p2 is greater than 1, consumed 2 will still consume 1 unit of good 1 and then move onto consuming good 2

I'll explain.

We have assumed p1>p2
Say p1=1 and p2=0.5
Now as you said consumer2 will want to consume y2=2/p2=2/0.5= 4. Which means if the economy had an allocation of 4 units he would have consumed 4, but as there is only 1 unit, he is restricted to consuming 1.
Ok. Now see he tells consumer 1 that in exchange for one unit of y from consumer 1 he would give him 0.5 unit of good x, which consumer 1 will accept (MRS). So the allocation changes from (0,1), (2,0) to (0.5,0), (1.5,1).
Now this allocation is a competitive equilibrium.
As a verification you can see that both are on higher indifferent curves and the value their respective endowments are the same as before.
So you can see that for any p1 >= p2, a competitive equilibrium will exist......

[duck]

Hi n.Saish.. :)

I think you are interpreting Competitive Equilibirum incorrectly!
The following is the definition>
For the given economy, a competitive allocation is that allocation where,
1>for a given price, each consumer is maximising his utility such tht value of endownmnt equals value of good they are demanding.. and
2>demand = supply for all commodities.. (or markets clear)


Just understand this definition and then try to think the way Aditi has done.

[aditi5000]

Hi n.saish! we say y1+y2 = 2/p2 = 1 and hence p2=2 not so that
so that consumer2 can consume the entire allocation of y in the economy
but because for markets to clear we need demand = supply in the economy. as you are aware, y1+y2 = 2/p2 is the total demand and 1 is the total supply.
Hope this helps :)

[tim]

hey guys cn u pls give the logic how did u get d) for q31..

[n.saish]

Thanks Guys, I re-read the definition of competitive equilibrium, it is where the markets clear.... So what you're saying seems correct..
But it still seems logical that the consumers will move to that new allocation I've mentioned... It benefits both and leaves them with the same value of the endowment... Unless they cannot exchange non integral amounts....

I feel that when you say that the market has to clear, it refers to the case where...
Say the in the economy x=10 and y=5
Say consumer 1 demands (4,1) and consumer 2 demands (3,2), here in this case is where the market not clearing concept comes into picture, as the can never exist one point in the edgeworth box where both would agree to consume...
So in this case the auctioneer would have to adjust the prices for the competitive equilibrium will exist.

But in the case of Q.32, although the demand of y is exceeding the supply, both are agreeing on a common point (as I've explained), won't that be a competitive equilibrium?

[aditi5000]

when either there is excess supply or excess demand for a commodity, competitive equilibrium doesnt  exist at those prices and thus the auctioneer moves on to the next set of prices and so on.. sometimes, we can find a price level where markets clear, as in this question. but sometimes, at  all price vectors, the agents' net demands don't equal zero.. So competitive eqbm may or may not exist.. here it exists at p1/p2=1 and we need to rule out the other possibilities by contradiction
at p1>p2 (the situation you mentioned) a2 only consumes good y because he treats x,y as pft substs so y2=2/p2 and x2=0 whereas a1 lexicographically prefers x to y so x2=p2/p1 ie entire income spent on x (unless between 2 bundles, x is same and only then y cms in2 the picture) and y1=0
adding y1 and y2 = 2/p2 and.... FOR MARKETS TO CLEAR (the condition the auctioneer puts) THIS NEEDS TO EQUAL resource of the economy =1
here this gives p2=2 ie a contradiction from our assumption p1>p2 Thus, our assumption that p1>p2 clears the mkt is wrong.
i hope you are convinced :)

[n.saish]

Ya... I guess so...
If your saying that the markets of each good must clear, then ya.. your correct...
Thanks a lot

[aditi5000]

And Walrasian law also asserts that so long as the market for one good clears, the other will also clear. So here at p2>p1 the market for y doesn't clear => market for x also won't clear!
You're most welcome :)

[Rain Man]

Hi

If an agent lexicographically prefers Good A to Good B , then she will spend all her income purchasing Good A unless the price of Good B is zero when she can buy any amount of Good B to maximize her utility. Is that right ?

Please help.

Thanks in advance

[n.saish]

Yes!!! The Walras' Law makes things very clear.
Really appreciate your efforts, Aditi, for convincing me out :)

[n.saish]

Hello Rain Man, I didn't exactly get what you want to ask, but I'll explain what is the meaning of Consumer 1 lexicographically prefers A to B.
Suppose there are two bundles a consumer has to choose from, then....
If a bundle has more of good A, she will prefer that bundle irrespective of the amount of good B present in that bundle.
If the two bundles have the same amount of good A then she will prefer the bundle with the greater amount of B.
Eg.
(3,2) > (2,20) but
(3,20) > (3,2)
I hope I've answered your question...

[aditi5000]

:)

[vikram]

Hey, great discussion!

I didn't understand why aditi has taken y1=0 in the first case of p1>p2. In the figure above, pareto efficient points include the vertical part marked red. So, how can it be assumed that y1 will be 0?

[vikram]

sorry, it's fine , i got it.