DSE 2013 Paper Discussion

[Granpa Simpson]

Series 1 or Series 4..??

[Granpa Simpson]

Q41) The consumer will be indifferent between the two bundles if the utility derived under optimum situation is equal in bothe the cases.
Now consider case 1: the optimum demand bundles are x1=x2=M/(p1+p2)=M/3.
In case 2: M=px*X+py*Y,
or, M=1*X+(2-θ)*Y+T.
or, M-T=1*X+(2-θ)*Y.
The optimum bundles in this case is given by x1=x2=(M-T)/(1+(2-θ))=(M-T)/(3-θ).
Utilities will be equal implies, M/3=(M-T)/(3-θ)......................(a).
from (a) we can derive, θ=3T/M (option b).
Q42) The consumer will borrow in period 1 only if (1+r)<=1/β,
r<=(1/β)-1, option a cannot be the answer as r will depend on the value of β, same is with option b, option c also cannot be the answer as derived, option d is the answer as it lies in the defined set r<=(1/β)-1.
Q49)Use the concept that for any point which is Competitive equilibrium the monetary value of the excess demand will be zero..this leads to the condition that the market gets cleared, so competitive a competitive price ratio will clear the market...now the question remains how to find that price ratio..under the assumption that the preferences are monotone, complete and convex a Pareto efficient bundle leads to a competitive equilibrium (second theorem of welfare economics)..now we know that a Lexicographic preference ordering is monotone, complete and convex so a choose a Pareto Efficient point and compare..in this case the initial endowment bundle is Pareto efficient (you can check that too). This gives.
px*10+py*0=px*0+py*10.
or, px=py.
or, px/py=1.
So option b seems to be the only answer because option a may or may not be true because px=py is true but it may or may not be equal to 1. Option c and d cannot be true because px=py, so both px>py and py>px are false..so option c suits best.

[SoniaKapoor]

Subhayu..pls guide me fr where to do intertemporal ?

[Granpa Simpson]

I think that for any of the Micro topics Varian is the best book from where you can get the concepts right..starting from Utility to Welfare (General Equilibrium)...going thoroughly between the lines and understanding the concepts is the best way which has been dealt in best manner in Hal. R. Varian..I think that will help you rather than going for any higher level text.

[SoniaKapoor]

thank you

[econ14]

hi Akshay for q 35. i am getting option (a) i.e always pareto efficient but the correct answer is (d) plz explain... thanx

[econ14]

@kangkan for q 38->
. (Suppose that a city can be described by an interval [0, 1].
Only two citizens, A and B, live in this city at different locations; A at 0.2
and B at 0.7. Government has decided to set up a nuclear power plant in
this city but is yet to choose its location. Each citizen wants the plant as
far as possible from her home and hence both of them have the same utility
function, u(d) = d, where d denotes the distance between the plant and home.
Find the set of Pareto optimal locations for the plant.
(a) All locations in the interval [0, 1] are Pareto optimal
(b) All locations in the interval [0.2, 0.7] are Pareto optimal
(c) 0.5 is the only Pareto optimal location
(d) 0 and 1 are the only Pareto optimal locations)

b must be the correct any idea....???

[Akshay Jain]

suppose that A's utility function is U(d)a=da and utility function of B is U(d)b=db
where da = |plant location in [0,1] - 0.2| and db = |plant location in [0,1] - 0.7|

If the plant is at extreme position say 0 den da= 0.2, db=0.7 and when plant is at extreme position 1 dn da=0.8, db=0.3

now take a plant location in interval (0,0.2) dn
da<0.2 and db<0.7, so both of them are worse off (position 0 pareto dominates (0,0.2)

similarly take a plant location in interval (0.7,1) dn
da<0.8 and db<0.3, so both of them are worse off (position 1 pareto dominates (0.7,1)
therefore option (a) is ruled out

now take a location 0.5 dn
da=0.3 and db=0.2 which means utility of A increases but dat of B decreases when compared with location 0 but it is pareto dominated by location 1 so option b and c are also ruled out


hence option D

[kangkan]

@Akshay..the question on heteroscekadascity..question 49 of series 1....

Accd to the big formula in gujrati(Appendix of chapter 11 page 434),the estimated vale of Sigma Hat is an unbiased estimator of sigma regardless of its relation to X(i)...but accd to answer key of of Amit Sit,it is option C...am i interpretting the the result wrongly?

[Akshay Jain]

Yes it is option c
but m not getting what is your doubt exactly???

[kangkan]

Hi...gujrati page 396 says that var B hat is a biased estimator of Beta in case of heteroskedascity...

[kangkan]

var (B hat)= sigma (xi^2)(si^2)/(sigma xi^2)^2  where s is sigma for variance

[kangkan]

And alrenately,if Z is variable that sytematically effect the variances of ui and has been left out,isnt the model underfitted?and if its undefitted,accd to what i cud make out from gujati(whcih  isnt a lot :( ) ,is that that variance of sigma hat will be a biased estimator of actual sigma

[neha:)]

Please help me with Q 42, 45, 54 and 55. (Series 1)

[ViV]

Q.54, C=0.25x, D=0.75x, and R/D=0.20, also C/D=0.25/0.75, now money multiplier=(C/D+1)/(C/D+R/D)=[(0.25/0.75)+1)/(0.25/0.75)+0.20)]=0.25...so increase in money supply=2000*2.5=5000 units.

Q.55 take LM curve vertical in exogenous case and upward sloping in endogenous case. You will find (c) as your answer.
Rest even I don't know...

Plz reply if u know any of the answer..
http://discussion-forum.2150183.n2.nabble.com/DSE-2013-Doubts-td7590991.html#a7591065 

[phelps.phan]

Hi Neha,
Q 42: Just find the total expected value.
P(Two 1 dollers)=6/20
P(One 1 doller, One 4 doller)=6/10
P(Two 4 dollers)=2/20

Expected value is (6/20)*2 + (6/10)*5 + (2/20)*8=4.4


Q 44: Total ways of forming the group without restriction= 5C2 * 5C3=100
The number of ways of forming a team with Mrs.F and Mr.M in the team is 4C1 * 4C2=24
(assume M and F are alredy in the team and u have to choose the remaining team members).

Total ways of forming the group without F and M in the team=100-24=76

[neha:)]

@ Viv and Phelps : Thanks a lot!

[neha:)]

How to do 58th? series 1..

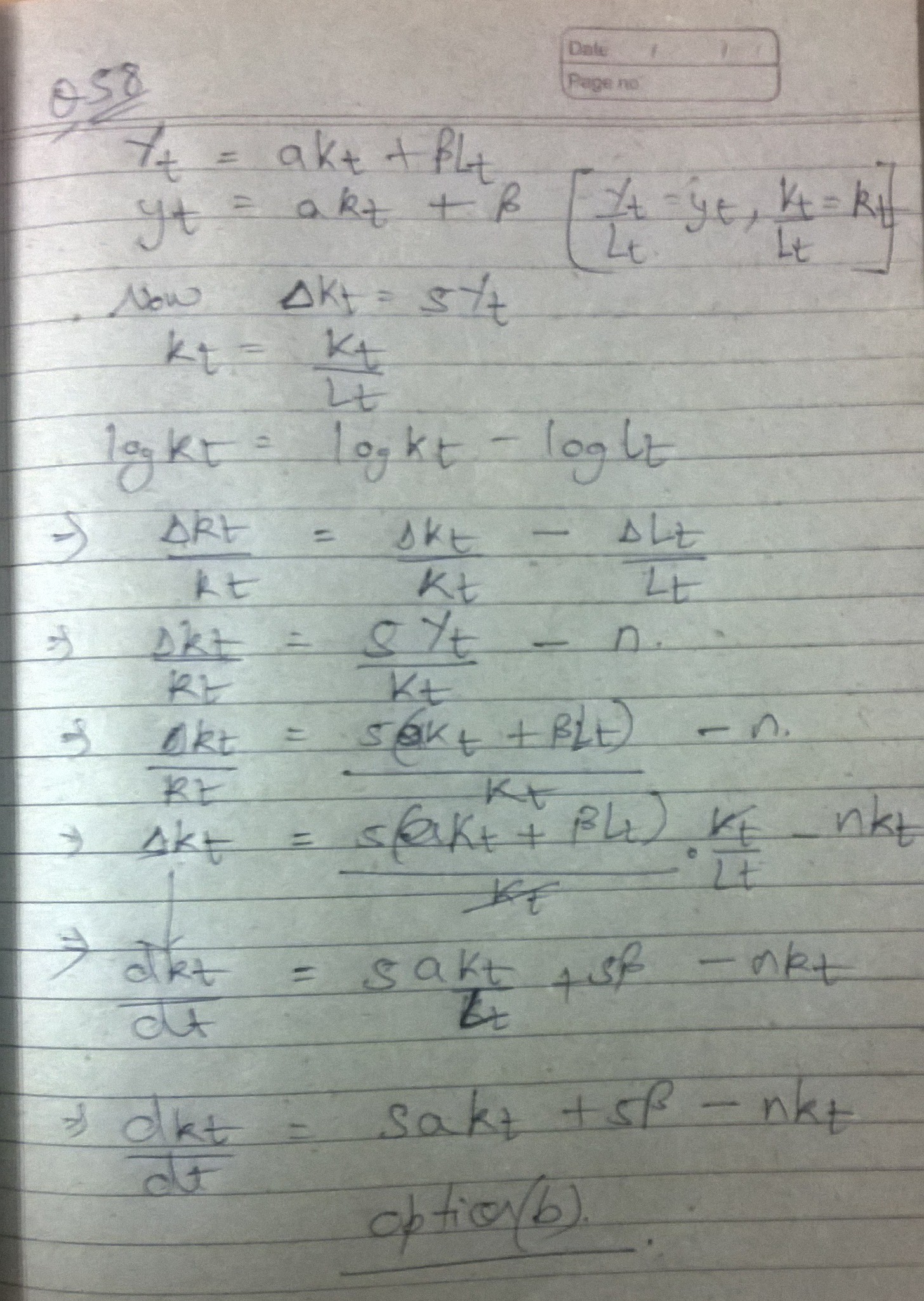
[Akshay Jain]

[xyz123]

Thanks a lot! Really helpful!

Can you explain the next step after the log equation?