Divisibility of the sum of squares of two odd numbers

[RichaS]

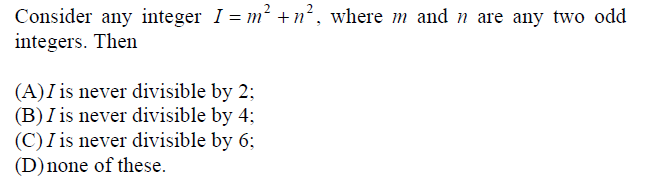
We need to find out of this integer is divisible by 2,4 or 6. I don't know how to start solving this.

Square of any odd number will have an odd number in the units place, and the sum of two odd numbers will yield an even number in the units place.

So the result will have an even number at the units place and will definitely e divisible by 2.

How to find out about 4 and 6?

[Amit Goyal]

Write m as (2p+1), and n as (2q+1), then

(m^2) + (n^2) = ((2p+1)^2) + ((2q+1)^2)

Expand it and you will get the following form: 4(expression) + 2
So, we can infer that the term is never divisible by 4.