Hybrid utility function

[RichaS]

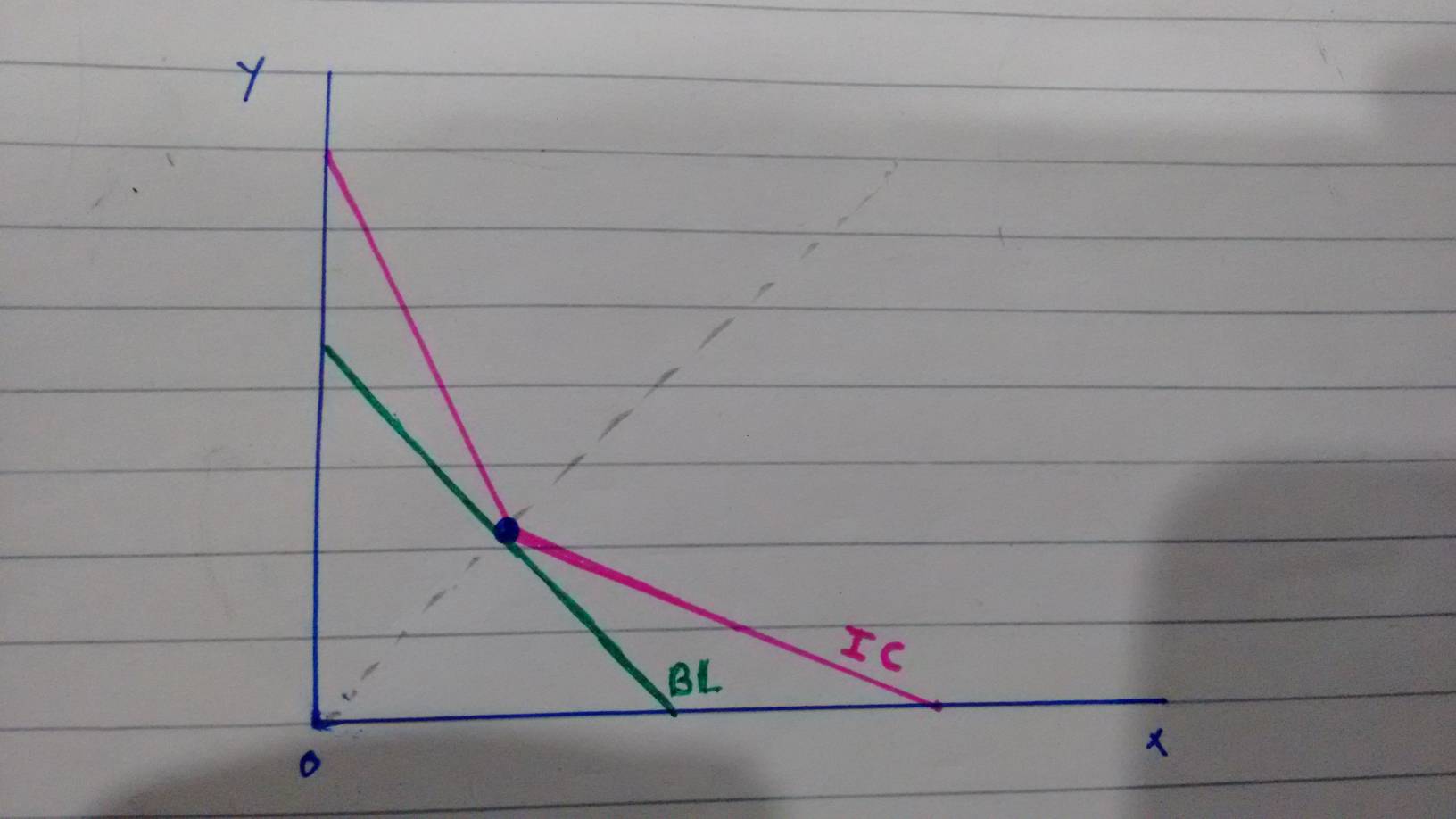
Consider the utility function u(x; y) = min(2x+y; x+2y)
 If neither x and y is equal to zero, and the optimum is unique, what must be the value of x/y in optimum?


Is this approach correct: x/y should be equal to MUx/MUy, which at the kink in the utility function lies amywhere between 1/2 and 2. Does the unique solution lie on the kink?

[Abhitesh]

Since the function is not differentiable at the kink, therefore MUx and MUy does not exist there.
Now the utility u(x,y) = min(2x+y, x+2y)
There can be three scenarios.
(I) As shown in the fig. (attached in question).
The BL is such that utility maximization occurs at the kink where 2x+y=x+2y
=> x/y =1

(II) Now suppose that the prices of x and y are such that px/py = 1/2. Taking x as numeraire,
BL will be x+2y=m. In this case BL will overlap with IC(x+2y) in which case x/y will depend upon their exact values.

(III) Similarly when px/py = 2.

[RichaS]

Thankyou!