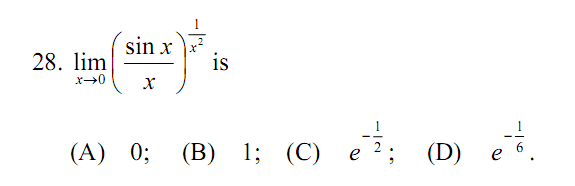ISI 2004 ME - I Answer Key

[Amit Goyal]

ISI 2004
1 a
2 b
3 c
4 a
5 c
6 d
7 b
8 c
9 c
10 a
11 d (the series converge to 1 which is not a number between 0 and 1)
12 c
13 c (There is a typo in the problem, I have computed x(∂u/∂x) + y(∂u/∂y))
14 d
15 c
16 a
17 b
18 c
19 b
20 a
21 b
22 d
23 d
24 a
25 c
26 c
27 a
28 d
29 d (ab ≠ 2a + b - 2)
30 b

[AJ]

How do we solve 30th question? I am getting (a) for it............

[lovekesh]

It's b only. Consider x=-4 and x=-1
at -4, it's negative and at -1, it's positive.
rest first order derivative says it ahs stationary values at -1 and 1. But at those ponits and even between them, it never cross x-axis.
Cheers

[AJ]

Thanks.. got it.. I just assumed that  min is at +1.. so value is never negative.. :p

and Have u been able to solve Q no. 12th and 28th .. ????
I am putting questions here for convenience...

12. Consider the function..
f(x)= (x^t-1)/(x^t+1) ... (x>0)

The limit of the function as t tends to infinity;
(A)  does not exist;  (B)  exists and is everywhere contin
(C)  exists and is discontinuous at exactly one point;
(D)  exists and is discontinuous at exactly two points.


28.

[ritu]

hi aj:)
for 12th question by l"opital rule u can clearly see that limit is always 1 barring the case when x is itself 1...in that case limit is 0....so limit exists everywhere and discontinuous at only one point...:)


sry but i spent hours on next question using log nd lopital but to no avail...:((

[ritu]

pls tell me how u solved 11 and 21:)

[AJ]

ohhh..its asking if limit is continuous.... I was checking continuity of function... :/

and for 11th..

1.1/2 + 1/2.1/3 + 1/3.1/4 + ...........1/n.1/(n+1) .....

each of these terms become... like 1/n-1/(n+1)
(1-1/2)+(1/2-1/3)+(1/3-1/4) .....

so adjacent terms will cancel.. like -1/2 with 1/2 .... leaving only the 1 in beginning..  
so series converges to 1....


and for 21st..
I don't know how to do this minimum distance questions..so, my solution is super clumsy...

so what i did was...I drew this y=x^2 curve ..and the line .. y=2x-4....

and saw all the options... like see the distance between line and these points..
and marked the one that looked minimum ... :p
so.. both (1/2,1/4) and (1,1) .. looks like the answer...

so... cant draw graph here.. but we need the length of perpendicular from given line to these two points..
for this we need the point on line from where the perpendicular starts...

lets take point (1,1) first... our given line had slope of 2..so thats tan theta..
and perpendicular has slope tan(90+theta) = -tan theta = -2

so we have slope of perpendicular..i.e. -2... and a point on perpendicular.. i.e. (1,1) ..
so equation becomes.. y=-2x + 3

and intersection of this perpendicular and given line gives us the point on first line from where the distance has to be measured... the point is.. (7/4, -1/2) .. and distance is 720/16^2...

I did same for point (1/2, 1/4) ... and got the distance as .. (1021/16^2) ... so 1st is less.. so that's the answer .. (1,1)
I tried my best to explain this.. hope u get it..

p.s.: i just did calculations again, so they might be wrong.. .. but that was what I basically did..
and if u find some neat way to do it..do temme!
:)

[lovekesh]

The answer is (d) for Q. 28
take exponential and write it like e^{ 1/x^2[sinx-x]/x}
u use sinx series
sinx= x-x^3/6+.....
answer is d only.

[ritu]

hi aj..:) well that was fab...but fortunately i have got a shorter method....
we have a formula of perpendicular distance from a given point to a given line....
D= { ax+by+c/under root a^2+ b^2}    this whole expression is within mod
now can take the point on curve as (x1,y1)
since this given point lies on y=x^2....we have y1=x1^2
put these values of (x1,y1) for (x,y) and u get D in terms of x1 only....now just minimise d nd u get x1=1 which implies y1=1

hope u find it crispier..:PPP

[aditi5000]

Hey how did we find the solution for question 3 about real roots? Please help.

[AJ]

@ritu.. ahhhh awesome...!!!  (I just found these smileys and love using 'em)

@aditi...

take derivative... its always +ve.. function is strictly increasing.. so passes through x axis only once...

[AJ]

Please explain Q.no. 5 ?

[aditi5000]

Hi, I meant question 3 not 30
f(x) = (x-a)^3 + (x-b)^3 + (x-c)^3
the number of real roots for f(x) = 0 is
A. 3
B. 2
C. 1
D. 0

[AJ]

Hi, I also meant q.no. 3

f'(x) = 3(x-a)^2+3(x-b)^2+3(x-c)^2

f'(x)>0

therefore, function is strictly increasing...
So, it can cross x-axis only once...

[aditi5000]

Perfect, got it. Thank you so much :)

[AJ]

:)

[archita]

plz explain question 28 again.....
i didnt get expresiion e^{ 1/x^2[sinx-x]/x} ,,,sholudnt it be e^[1/x^2*ln (sinx/x)]  ?

[Chinni18]

Question no.5 @ AJ
From equation (i) we have:
y = 2 + 3x and x = -2/3 + (y/3)
The regression coefficients beta_yx and beta_xy are respectively 3 and 1/3
Therefore correlation coefficient rho would be simply the square root of product of the beta's i.e 1
Similary for equation (ii), you get the beta values as 4 and 1/4, the product of which yields 1 again.
Hence option (C)

[duck12]

Can someone plz help with Q.15

[AJ]

Like this... wont we always get 1 as the product of both regression coefficients..??

we take 1 equation.. if its linear..

bxy is simply slope when y is dependent..
and byx is slope when x is dependent.... so both will be inverse of each other...

product will always be one.....