Jnu 2005
|
For an economy , the long run rate of growth of GDP is 5% per annum at full employment. The investment rate is 20% and the rate of growth of labour force is 2% per annum. Then the capital output ratio is
2 5 7 10
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
k ( capital per worker) = K/L
Taking ln both sides will give: ln k = lnK - ln L Differentiating wrt time gives (dk/dt)/k = (dK/dt)/K - (dL/dt)/L Now , dK/dt is investment which can be written as s*Q Which gives, rate of growth of capital = (s*Q)/K - rate of growth of labour In the long run equilibrium, the rate of growth of capital is zero. We are given that output is growing at 5% p.a. and labour force growth is contributing to it by 2% only, rest 3% could be from anywhere else. But using the equation of Harrod Domar model, we have to let rate of growth of capital to be zero. there is no use of rate of growth of GDP here . we just have to use the equation which will give: (s*Q)/K = rate of growth of labour implies K/Q = s/rate of growth of labour = 20%/2% = 10 This is what i think should be the answer, it might be wrong also !! |
|
Hi arushi !
Well why can we use the standard harod domar equation here , which is g+n+dep of capital ( here 0 ,I suppose ) = s/Q Now s= S/Y , and q= K /Y why can't we equate s ( saving rate ) with investment rate ( 20 % ) ? Your answer could be right , however I did not get what you have explained here. Please guide.
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
i have also used harrod domar equation only, in a little different way.
See here we are given 5% as the rate of growth of GDP But we can't use the equation s/theta= n+g because g is the per capita rate of growth and we are not given that, we are given the overall rate of growth of GDP. so to eliminate g i did'nt use the equation directly. In per capita terms , capital per worker = K/L If we want to see the rate of growth of capital per worker ; the usual procedure is taking natural logarithm and differentiate wrt time. That way we get rate of growth of per capita capital equals (dK/dt)/K - (dL/dt)/L Now dK/dt can be seen as change in capital with time, since we are assuming depreciation to be zero, we can solely take dK to be investment which equals saving on a period of time dt. So, dK/dt is the investment and now savings = investment ,we can write dK/dt= s*Q We can assume that in the long run capital won't grow, output can grow, but at the steady state capital won't change, so per capita rate of growth of capital will be zero in long run; which will give, (s*Q)/K= (dL/dt)/L RHS = 2% s = 20% implies K/Q = 10 . I hope you got it :/ |
|
Everything is fine , except for this
dK/dt= s*Q Dk/dt is the rate of investment , how can we equate it with an absolute value - s* Q ?
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
We can,
dK/dt is the change in the capital stock over a period of time. dK/dt = Investment - depriciation over that period of time. since, we are given nothing about depreciation, we can say that it is zero and dK/dt>0 , because only investment is being done. so, dK/dt can be seen as investment . I know its little complicated, but i discussed it with my friends and we reached to this conclusion! |
|
So you mean that dk/dt is not the rate but the absolute level of investment ? I know dep is 0 , but more capital is also being added , so dk/dt = 20 % . Is that so ?
And Iam still not clear that why you have equated dk/dt = s * Q
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
Okay , so i was initially using harrod domar equation and tried to eliminate g ( rate of growth IN PER CAPITA TERMS).
Now, what i got is, we can take advantage of solow model , forget harrod domar model, in solow model, we anyway have to consider everything in per capita terms, so that way if you agree with the thing that dK/dt = investment, we know that every economy converges to a steady state where capital per person doesnt grow, steady state capital is constant , so we can then put rate of growth of per capita capital equal to zero. then , you well get, s/ theta= rate of growth of labour force . The only thing to note here is dK/dt equals investment = s*Q(total amount of investment) change in capital over a period of time; and capital is only being added here !! so we can take it as absolute level of investment yaar.... I dunno where i m turning my analysis to. i am satisfied with the solow thing now. someone please help! |
|
Honestly it's really confusing.
In s* Q , Q ( theta ) = capital output ratio ? Or just output ? What , I ll do is that I ll go through solow model once again , and then I will try to correlate . I will get back to you in case of any doubt.
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
hey ! anjaliiiiiiiiiii.....
You were taking capital Q as theta till now !!!  see now, Q is total output ! Forget the whole discussion till now, start fresh! i ll just begin with capital per person, small K = k = K/L rate of growth of k= rate of growth of K - rate of growth of L ok? rate of growth of k = (dK/dt)/K - (dL/dt)/L Now , since in the long run , economy reaches steady state and at steady state rate of growth of k is equal to zero ( capital per person doesn't grow). this gives , (dK/dt)/K = (dL/dt)/L Now i can replace dK/dt by amount of investment done = savings rate x total output(income)= s * Q, where Q is the total income ( output). Next ,substitute this into the equation; we get Investment/ total capital = rate of growth of labour (s*Q)/K= 2% s/capital-output ratio= 2% we have s = 20% => capital-output ratio = 10. |
|
Lol ! This theta was actually making my life a little difficult :p
How is this (dL/dt)/L = rate of growth of labour ? Shouldn't it be just dL/dt ?
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
In reply to this post by Arushi :))
Aarushiiii ! :-)
Finally I have got it ! Read solow today , and now Iam comfortable with this question. From the same chapter , I have another task for you. Thanks a ton :-)
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
In reply to this post by Arushi :))
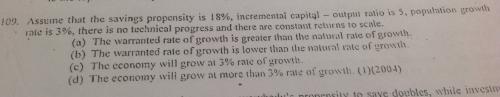
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
So the answer is 10??? in case the question gets repeated????
|
|
I don't know the answer
 But Your approach seems fine 
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
Haha.. :) I ll choose 10, if it comes :P
And for this question, http://financial-dictionary.thefreedictionary.com/Warranted+Growth+Rate this link says warranted rate of growth is savinga rate/ ICOR = 18%/5 = 0.036 And natural rate of growth of an economy is given by the population growth rate = 3%= 0.03 So warranted rate of growth> natural rate of growth . So a is the right option :) |
|
OMG it was that simple !
 Lol thanks again :-) Ya even I will go with 10 
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
Btw what is the difference between capital output ratio and ICOR ?
If we are given any question , based on harrod domar , and ICOR is given , so can we apply harrod domar standard equation ?
"Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth."
|
|
In reply to this post by Anjali
nai, it wasnt if we don't now how to calculate warranted rate of growth :P
Even i got it hen i googled it . :D And thanks for the probability question got it    |
«
Return to General Discussions
|
1 view|%1 views
| Free forum by Nabble | Edit this page |


