Joint pdf

[Devika]

f(x,y) = 2 for x>0, y>0 x+y<1
        = 0 otherwise

Find P( X+Y > 2/3)

I did as follows

Integral x= 2/3 to 1 Integral y= 2/3-x to 1-x   2dydx

Where am I going wrong? :s

Also, I'm having a really hard time solving such questions by plotting on the graph. I fail to get the right integral limits!! Help please :(

[Mauli]

hi devika!
i know !
i too fair poorly in these type of questions.
but tell me something.. have u seen the past years?
i have seen them till 2008.and i haven't come across these ''double integral'' type of questions much.
let me know if u have seen these type of questions somewhr in the dse pprs.

[Xiang]

can u please tell me the answer?

I would want to confirm the answer before explaining.
Thank you

[Mauli]

5/9 xiang!

[Devika]

Heyy Mauli,

Though I haven't come across such questions, but the only thing predictable about the paper pattern is that its unpredictable. x_x

[Devika]

Yes Xiang. Its 5/9

What did you get?

[Mauli]

right you are.but , still i rily dnt feel for it.
but then if thy would have been going by what i would have felt..
then they would have given answers along with the questions

[Xiang]

I am getting 2/3 O_O

[Sinistral]

here you dont need to actually integrate since f(x,y) is constant.

basically u need to find the area between red line and blue line.



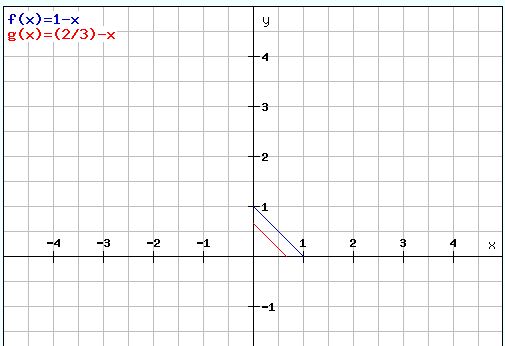
so find the area of the i bigger triangle and smaller triangle. subtract the two.
note that red line intersects x and y axis at 2/3
and blue line intersects x and y axis at 1.

so the required area will be 5/18

multiplying it with f(x,y) ie 2 will give 5/9

[Xiang]

looks cool!

thanks :D

[Mauli]

thanks dude:)
a great solution indeed!

[Xiang]

but if we integrate what will be the limits? O_______o

[Sinistral]

Integral (x=0 to 2/3) Integral ( y= 2/3 -x to 1-x) f(x,y) dy dx  + Integral (x=2/3 to 1) Integral (y=0 to 1-x) f(x,y) dy dx.

[Devika]

Could you please explain the latter part. The part after the + sign. Also, why do we add? :s

[Devika]

Hahaha. If only life was that simple :D

[Devika]

And thanks for the solution! :)

[Sinistral]

actually we need to integrate between the 2 lines ( x+y=1 & x+y=2/3) when x goes from 0 to 1.

so we first integrate from x=0 to x= 2/3 . here y goes from y=2/3 -x to y= 1-x

then we integrate from x=2/3 to x= 1. here y goes from y=0 to y=1-x

see the below image:

[Devika]

Oh. I think I'm starting to get it now. Will practice more.

Cannot thank you enough! :)

Thank you!