PDF- Sinistral, have a look.

[Devika]

CONTENTS DELETED

The author has deleted this message.

[Sinistral]

The below solution is not correct. The final and correct solution (verified by Amit Sir) is in the 2nd last post of this thread.

I dont think U and V will be independent since both depend on X and Y.

F(u,v)= P(U<u, V<v)= P( U<u, V<v  | X<Y) + P(U<u, V<v  | X>Y)
    since X can be either greater than Y or less than Y
        =P ( X<u,Y<v) + P (Y<u,X<v)
        =P( X<u)*P(Y<v) + P(Y<u)*P(X<v)  since X and Y are independent.
         = Integral (x=0 to u) 2x^2 dx * Integral(y=0 to v) 3y^3 dy   + Integral(y=0 to u) 3y^3 dy * Integral (x=0 to v) 2x^2 dx
         =u^2*v^3  + v^2*u^3
         
f(u,v)=  ∂²F(u,v)/∂u∂v
        = 6uv(u+v)      0<u<v<1


 

[Devika]

Uffff. Forgot to make the two cases. x_x

Thanks a bunch!!

[MR]

Hey Devika,
 If possible can you please re post the question? :)

[Sinistral]

u shudnt have deleted that. because ur method of calculating f(u) and f(v) was correct. But I cant think of a way of going from marginal pdfs to joint pds if the random variables concerned are not independent.

[Devika]

Let X and Y denote independent random variables, with the following pdf-

f(x) = 2x  0<x<1
      = 0 otherwise

f(y)= 3y^2
     = 0 otherwise

Let U=Min {X,Y} and V=Max{X,Y}

Find the joint pdf of X and Y.

[Devika]

I deleted because I thought my solution would mislead and baffle others. Also, I took U and V to be independent, and hence multiplied the marginal densities to get the joint pdf.

[rohan]

@Sinistral
F(u,v)= P(U<u, V<v)= P( U<u, V<v  | X<Y) + P(U<u, V<v  | X>Y) ????ye kaise strike kiya..grt way

[Amit Goyal]

This is incorrect:
F(u,v)= Pr(U<u, V<v)= Pr( U<u, V<v|X<Y) + Pr(U<u, V<v|X>Y)

The correction is:
F(u,v)= Pr(U<u, V<v)= Pr(U<u, V<v|X<Y) Pr(X<Y) + P(U<u, V<v|X>Y) Pr(X>Y)

Now redo it.

[Sinistral]

Oh yes!! how could I miss that. (thank you so much Sir)

EDIT
F(u,v)= Pr(U<u, V<v)= Pr(U<u, V<v|X<Y) Pr(X<Y) + P(U<u, V<v|X>Y) Pr(X>Y)   (as pointed by Amit Sir and now it seems fairly obvious).
                              Pr(U<u, V<v AND X<Y) * Pr(X<Y)     +    P(U<u, V<v AND X>Y) * Pr(X>Y)
                         =   --------------------------------          ----------------------------
                                        Pr(X<Y)                                                   Pr(X>Y)


                         =               P ( X<u,Y<v)                     +                P (Y<u,X<v)
/EDIT

Rest of the solution is same:

        =P( X<u)*P(Y<v) + P(Y<u)*P(X<v)  since X and Y are independent.
         = Integral (x=0 to u) 2x^2 dx * Integral(y=0 to v) 3y^3 dy   + Integral(y=0 to u) 3y^3 dy * Integral (x=0 to v) 2x^2 dx
         =u^2*v^3  + v^2*u^3
         
f(u,v)=  ∂²F(u,v)/∂u∂v
        = 6uv(u+v)      0<u<v<1

[Amit Goyal]

There is still a mistake. Because U<u, V<v AND X<Y implies that X< u and Y < v but is not implied by it. Hence {U<u, V<v AND X<Y} is not the same event as {X<u,Y<v} but is a subset of it and you can't replace {U<u, V<v AND X<Y} by {X<u,Y<v}

[Sinistral]

Ques: X and Y are independent rv
f(x) = 2x  0<x<1
      = 0 otherwise

f(y)= 3y^2  ; 0<y<1
     = 0 otherwise
U=Min{X,Y} & V=Max{X,Y}. Find joint pdf of U and V.
-----

f(x,y)= 6xy^2 ; 0<x<1 &  0<y<1  (since X and Y are independent)
        = 0        ; elsewhere.

F(u,v)= Pr(U<u, V<v)= Pr(U<u, V<v|X<=Y) Pr(X<=Y) + Pr(U<u, V<v|X>Y) Pr(X>Y)
                              Pr(U<u, V<v AND X<Y) * Pr(X<=Y)     +    Pr(U<u, V<v AND X>Y) * Pr(X>Y)
                         =   --------------------------------             ---------------------------------
                                        Pr(X<=Y)                                                   Pr(X>Y)

                         =  Pr(U<u, V<v AND X<=Y)                   +          Pr(U<u, V<v AND X>Y)
                         = Pr(Min{X,Y}<u, Max{X,Y}<v AND X<=Y)  +  Pr(Min{X,Y}<u, Max{X,Y}<v AND X>Y)


Pr(Min{X,Y}<u, Max{X,Y}<v AND X<=Y)  :</b>


 Pr(Min{X,Y}<u, Max{X,Y}<v AND X>Y):


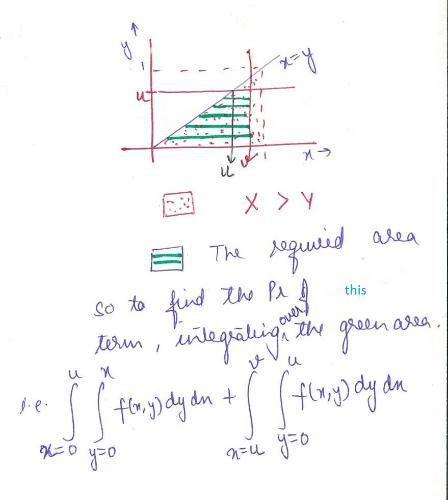
Adding the above 4 integrals would give Pr(U<u, V<v)=F(u,v);  [Assuming U<=V since Min(X,Y) <= Max(X,Y)].

[Amit Goyal]

Now this is correct. Good.