mathematics (Plz help)
 ********************************************************************************  ******************************************************************************** I am getting c as my answer. what is the correct ans? and why?  ******************************************************************************** in the ques below i know (i) is true but what can be inferred about (ii)??  ******************************************************************************** I know F"(x)>0. So it shud be concave upwards. So option a will be correct or b? 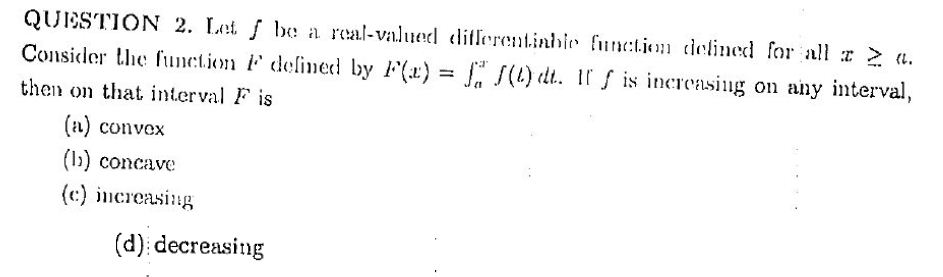
---
"You don't have to believe in God, but you should believe in The Book." -Paul Erdős |
|
Hi Sinistral.. :)
Q1) f is a real valued function ....such that f(xy)=f(x)+f(y) for all x,y in domain... Answer: Since, the above condition holds for all x,y in the domain. It must hold for "1" and "1/x". ⇒ f(1/x) = f(1)+f(1/x) It can only hold when f(1)=0. Similarly, you can show f(-1) must be zero. Hence, f(1)=f(-1)=0. Now, lets show the second condition: The given condition will hold for "x" and "1/x". ⇒ f(1)= f(x)+f(1/x) ⇒ f(x) = f(1/x)...... (I) The condition also holds for "-x" and "1/x". ⇒f(-1)= f(-x)+f(1/x) ⇒f(-x)=f(1/x)........ (II) From (I) and (II) we've: f(x)= f(-x) for every x. Hence, proved.
:)
|
|
In reply to this post by Sinistral
I need help with these too.
For the third question, option (c) is correct as per the answer key. Could someone explain to me when g is not increasing in y? For the second question, I think that only the second statement is true. For the second last question, is it conceptually wrong to do this? f(-x) = f((x)(-1)) = f(x) + f(-1) = f(x). Also, concave upward means that the function is convex. |
|
In reply to this post by duck
thank you Mr Duck :)
---
"You don't have to believe in God, but you should believe in The Book." -Paul Erdős |
|
In reply to this post by Do bats eat cats?
which answer key? could you please post the link to it. I checked for two values of y keeping x as constant (both above the line y=x and below the line y=x). It didnt show an "always increasing behaviour" wrt y. Doing the same thing wrt x (keeping y constant) in both the regions shows that f increases wrt x. I was looking for a more formal way to do this. thanx a lot for clearing that convex concave doubt :)
---
"You don't have to believe in God, but you should believe in The Book." -Paul Erdős |
|
please help with the first 2 questions(in the very first post) as well.
and in the following question: I know what to do but can some one plz tell me how to do it? My method is taking a lot of time. 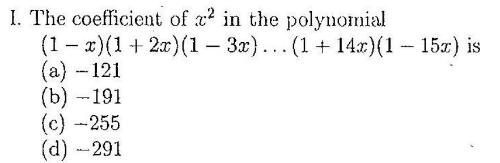
---
"You don't have to believe in God, but you should believe in The Book." -Paul Erdős |
|
In reply to this post by Sinistral
For the last one use Leibniz integral rule. Or you could draw a figure and interpret the integral as area under the curve.
|
|
In reply to this post by Sinistral
I'm assuming that you're looking at option B papers. Most of these questions are in Option A as well. The third question is the 54th question in the 2010(A) paper.
|
|
In reply to this post by anon_econ
yeah. I used that only. I was confused if concave upwards is convex or concave downwards is convex. I think now that doubt is cleared.
could you please help me with the first 2 questions as well.
---
"You don't have to believe in God, but you should believe in The Book." -Paul Erdős |
|
In reply to this post by Do bats eat cats?
thank you.
I think I went through the mathematics questions of Option A a couple of months back. No doubt now I am having Deja Vu when I am attempting option B objective questions.
---
"You don't have to believe in God, but you should believe in The Book." -Paul Erdős |
|
In reply to this post by Sinistral
I have no idea about the first question and have a somewhat confused (and possibly inaccurate) solution for the second question, so read this at your own discretion.
Statement 1: Can be disproved with an example. I used the greater than relation. It is both transitive and negatively transitive. Statement 2: R is transitive. If (x,y), (y,z) and (z,x) ∈ R, then by the definition of R(-1), (y,x), (z,y) and (z,x) ∈ R(-1). Or, (z,y) and (y,x) ∈ R(-1) and so does (z,x). So R(-1) is transitive too. Statement 3: R is transitive As per statement 2, this means that R(-1) is transitive too. So the statement reduces to if R(-1) is transitive, then it is also negatively transitive. Again I used an example (the equal to relation) to check that this is not true. Equal to is transitive but not negatively transitive. I suspect that all reflexive relations that are transitive are not negatively transitive, but I'm not too sure. |
|
In reply to this post by Sinistral
Hi.. :)
For Transitivity question: Only statement (b) is correct. If R is transitive then R-(1) is transitive. To show: If (x,y)∈ R-(1) , (y,z)∈ R-(1) then, (x,z)∈R-(1) Proof: (x,y)∈ R-(1) implies (y,x)∈R and (y,z)∈ R-(1) implies (z,y)∈R By transitivity of R, (z,x)∈R implying (x,z)∈R-(1) Hence, proved. Statement (a): Counter example: R={(x,z) ; (x,y)} Statement (c): Counter example: R={(z,x)} And its Ms.Duck.. :)
:)
|
|
This post was updated on .
my apologies.
and yes thanx a lot Ms duck. :) You are so marvellous at proofs. I want to ask a general doubt wrt proofs: Suppose I want to prove a statement, lets say To Prove: E[X^p] = Integral px^(p-1)[1-F(x)] (just an example). now can I start with this statement ( to prove statement) and move ahead till I get a statement which everybody knows is true. Like in the above example if after a few steps I get E[X^p] = Integral [x^p* f(x)dx] then will the prove be done? Is starting from "to prove" statement (and NOT from "given statement" or NOT from "a statement known to be true") is a right procedure?
---
"You don't have to believe in God, but you should believe in The Book." -Paul Erdős |
|
Hey Sinistral.. :)
That depends upon the statement to be proved. Suppose, i want to show If A then B. Now, i can do this using the following ways: (1) Take antecendant as given and then deduce B from it. (2) Take antecedant as given, assume B to be false and reach some contradiction. (3) Prove the contrapositive. Sorry, I couldn't understand this part: "lets say To Prove: E[X^p] = Integral px^(p-1)[1-F(x)] (just an example). now can I start with this statement ( to prove statement) and move ahead till I get a statement which everybody knows is true. Like in the above example if after a few steps I get E[X^p] = Integral [x^p* f(x)dx] then will the prove be done?"
:)
|
|
what i meant was suppose its given, prove A.
That example I was talking about is DSE 2012 Option B Ques 15(A) I started from the statement which needed to be proved and then I reached at: E(X^p) = Integral [x^p*f(x) dx] -- which is the formal definition of E(X^p). so is this kind of procedure acceptable?
---
"You don't have to believe in God, but you should believe in The Book." -Paul Erdős |
|
No.. Start with the formal definition and then reach whatever needs to be proved.
The method you're using actually assumes "to be proved" statement true.. So it doens't make any sense as we need to prove that.. :)
:)
|
|
oh.. & there I was thinking this question is so obvious.
while proving the other way round can I just retrace my steps??
---
"You don't have to believe in God, but you should believe in The Book." -Paul Erdős |
«
Return to General Discussions
|
1 view|%1 views
| Free forum by Nabble | Edit this page |

