prob doubt

[Akshay Jain]

Suppose that two persons make an appointment to meet between 5 p.m. and 6 p.m. at a certain location, and they agree that neither person will wait more than 10 minutes for the other person. If they arrive independently at random times between 5 p.m. and 6 p.m., what is the probability that they will meet?

a)     7/16

b)    9/16

c)     11/36      

d)    25/16

[PBANSAL]

how is the variable distributed? uniformly?

[Do bats eat cats?]

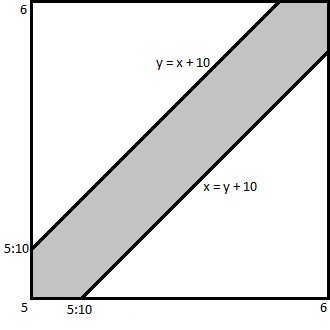
There is a way to solve this question graphically.

Plot the time of arrival of person 1 on the x-axis, and that of person 2 on the y-axis.
The line y = x + 10 corresponds to all times when the person 2 arrives 10 minutes after person 1.
Similarly, the x = y + 10 corresponds to all times when the person 1 arrives 10 minutes after person 2.

The area in the square bounded by these two lines represents all the times when the two persons will arrive within 10 minutes of each other.

The area of the square is 60 × 60 = 3600.
The area of the grey region is the area of the square minus the area of the two triangles, which is 3600 - 2(1/2)(50)(50) = 1100.

So, the required probability is 1100/3600 = 11/36

[PBANSAL]

Bats it is correct provided its uniform.but looking at the options I think its uniform only.

[Do bats eat cats?]

The question is worded "they arrive independently at random times". I took that to mean that the arrival times are uniformly distributed. In retrospect, that was a bad assumption.
In case the times are not uniformly distributed, isn't the question incomplete?

[Sinistral]

I think it clearly means that X,Y~U(5,6). If not then they wont be coming in the given time interval "randomly". and if it was not uniformly distributed they would have given a distribution function. In that case we can always  integrate the given pdf over the "required area" i.e (X-1/6)<Y<(X+1/6) and 5<X<6 and 5<Y<6.