probability

[neha]

Three points are taken at random on the circumference of a circle, find the chance that they lie on the same semi circle.

[deepak]

The answer is 3/4



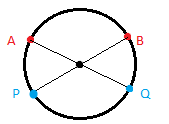
In the image attached above, let's assume that 2 points have been choosen - namely A and B (red dots). Now the point C can lie in any of the 3 upper arcs - PA, AB or BQ. ie, if it lies in the arc PA then the semicircle is PAB or APQ (depending on whether the point is above or below P) and similarly for the other 2 arcs. The only place where the 3rd point could be placed for it to not fall on the same semi circle is the bottom arc PQ.

Now if the angle between the radii to points A and B is x, the angle between the radii joining P and Q is also x.
P(3 points not in same semi circle) = P(3rd point in the arc PQ)
Remember that any 2 points will always lie in a semi circle, ie central angle between any 2 points on a circle varies from 0 -> pi
P(Angle subtended by any 2 points = x) = 1/pi (ie, out of pi possible values, we choose 1 value = x)
P(3rd point lies inside this range) = x/2pi (ie, out of 2pi possible values, we choose all values less than or equal to x)
So P(3 points lie inside the arc) = product of the earlier 2 probabilities (since they are independent)
P(3 points in arc PQ) = integral of [(1/pi) * (x/2pi) dx] between limits 0 -> pi = 1/4
ie, P(3 points not in the same semicircle) = 1/4
Therefore, P(3 points in the same semicircle) = 1-1/4 = 3/4