questions
|
Let f(x, y), g(x, y) : R^2 to R be scalar-valued multivariable functions. Determine what statements are true (i) If f has a local minimum at the point a, then f cannot have a local maximum at a. (ii) If a is a saddle point of f, then f cannot have a local extremum at a. (iii) If f has a local minimum at a and g has a local maximum at a, then a is a saddle point of f + g. Answer is (ii) ... but isn't statement (i) also true...??? OR is it that for a constant function every point is local maximum as well as minimum ...?? |
|
suppose z= f(x+y, x-y) has continuous partial derivatives wrt u=x+y and v=x-y then (dz/dx)( dz/dy) = (here d means partial derivative) (i) dz/du +dz/dv (ii) (dz/du) (dz/dv) (iii) (dz/du)^2 +(dz/dv)^2 (iv) (dz/du)^2 - (dz/dv)^2 I got (iv) .. I don't have answer! |
|
Suppose there are two states of the world: good and bad. In the good state of the world your income is $250,000. In the bad state of the world your income is $40,000. The good state occurs with probably .25 and the bad state occurs with probably .75. Suppose your utility function is: u = y^1/2 where y = income.
What would be an expected profit from“income insurance” contract if it took away all your income risk and left you indifferent between buying the insurance and taking the income gamble? (i)75,625 (ii)174,375 (iii)210,000 (iv)16875. I got, 16875, as the amount of insurance premium, such that we will be indifferent b/w buying the insurance and taking the gamble. But, is this amount "expected profit" ...??? |
|
And the next part of above question is:
Question 25. Suppose there are two states of the world: good and bad. In the good state of the world your income is $250,000. In the bad state of the world your income is $40,000. The good state occurs with probably .25 and the bad state occurs with probably .75. Suppose your utility function is: u = y1/2 where y = income. How would your answer change if the good state and bad state were equally likely? 90,000 160,000 210,000 55,000 ??? PLEASE HELP!!!! |
|
In reply to this post by AJ
AJ, the insurance contract leaves you indifferent between buying the cover and taking the income gamble. Therefore, your expected utility should be the same whether you buy the cover or not. That's possible with a premium of $174,375. The expected profit should, in fact, be $16,875, but how did you get it?
The answer to the second question is not in the options. Where are these questions from? |
|
@chocolate frog
I did this: Expected income is: 0.25(250000) + 0.75(40000) = 92500 Expected utility is : 0.25(500) + 0.75(200) = 275 Same utility can be obtained from a certain income of 275*275 = 75625 Therefore, maximum amount of insurance premium he will be ready to pay will be (92500-75625) = 16875 1. I did't get how u got 174,375 ... And what is this amount. 2. and, please explain what is expected profit here? like if we are indifferent between two alternatives, shouldn't then expected profit be zero..!!! And ya, me too not getting answer for 2 ques. as any of the options. They are papers from my coaching. The answers given many times are wrong..and like this not in options.. :( Any thoughts on first and second problem? |
|
AJ, you calculated the certainty equivalent correctly as $75,625, but the next step is incorrect.
Suppose you buy an insurance cover of amount K and pay a premium of p towards the cover. Then, if the insurance contract takes away your income risk and leaves you indifferent between buying insurance or not, you should end up with the same utility with or without the cover. Now, $75,625 given to you with certainty gives you the same utility as the income gamble. Therefore, the insurance contract should leave you with exactly that much, otherwise you'd choose the option that pays more. Mathematically, 75625 = 250000 - p, which gives you a premium of $174,375. Also, 40000 - p + K = 75625, which gives you a cover of $210,000. You're paying $174,375 with certainty, and paid $210,000 with probability 0.75. So, expected profit = 174375 - (0.75)*210000 = $16,875. Following through similarly on the next part, you'll get an expected profit of $22,500. |
|
This post was updated on .
In reply to this post by AJ
Q1. I'm not one hundred percent sure about this one. Actually, in three dimensional geometry, it is possible to have a local maxima in one plane and a local minima in another plane at the same point, but that's not the question, I'm afraid. :S
Q2. Your answer is correct. |
|
Chocolate frog..
Thankyou so much for explaining insurance problem. That actually cleared a lot of things. And for 1st.. How can we have local maxima in one plane and minima in other plane at same point. Won't that be infact a saddle point like in this figure 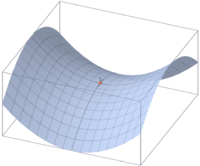
|
|
In reply to this post by Chocolate Frog
And, while we are at it, can u please see this too..
f:R^n to R is convex iff: (a) {(x,r)| f(x)<= r} is convex (b) {x belongs to R^n | f(x)<=r} is convex for every r belonging to R I just have to ask that these statements respectively mean (a) epigraph is convex set (b) lower contour sets are convex Is this right..??? So, (a) implies convexity and (b) implies Quasiconvexity Is this all right???? |
«
Return to General Discussions
|
1 view|%1 views
| Free forum by Nabble | Edit this page |

