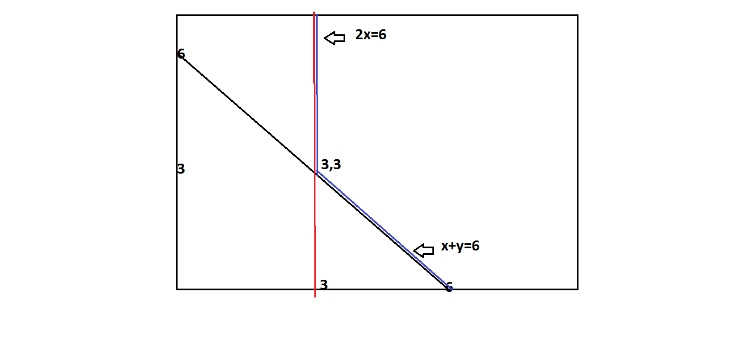
f(x,y) = min { 2x, x+y }
Let f(x,y) = 6,
then either of the terms i.e x+y or 2x = 6
=> we have to plot these two curves first;
1) x+y=6
2) 2x = 6 => x=3
Drawing these two, the graph consists of four portions;
On the line x= 3,
If we take the portion below (3,3)
eg: 3,1
then min ( 6,4) = 4 not equal to 6,
so all the points on 2x= 6 below 3,3 will be rejected.
Similarly,
all the points on x+y=6 to the left of 3,3
will have min not equal to 6.
All, the points in blue color will compromise the isoquant because on all those points min equals 6.