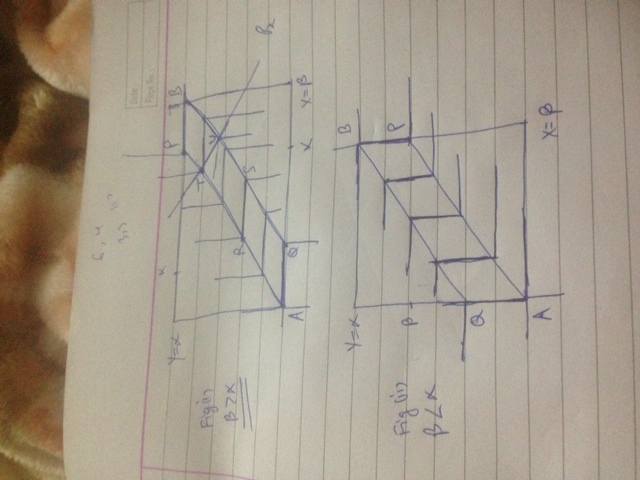
Refer to the fig. for solution.
In fig 1: beta(b)>alpha(a)
Here the pareto optimal allocations are all the points on AP and BQ as well as all the points inside it.
These pareto optimal points lie on the horizontal portion of the IC's of both individuals (say RS in the fig.). We know that in case of a min function, slope of horizontal line of IC is 0. For maximization price ratio must equal MRSxy=0 in this case. Thus, Price of x is zero. If you take any other price ratio say Px marked in the fig then each individual will be maximizing its utility at different points - T and U in the fig.
In fig 2: b<a
Here, pareto optimal points will lie on the vertical portion of the IC'S of both the individuals where slope is infinity. Hence, Px can not be zero.
One problem with the way you have solved is that you are taking x=y for both the individuals. But that can not be pareto optimal allocations. If each individual is at kink point then there will be always excess dd or excess ss.