JNU ECOM 2010 QUES 62-70

[Arushi :))]

The next three questions 62-64 are based on the following information:
A student has taken 5 courses: philosophy, biology, economics , mathematics & literature.
He studies for these courses according to the following pattern:
Every week the student studies for exactly three courses.
If he studies Biology in a week, then he also studies Philosophy that week.
If he studies Economics in a particular week, then he doesn't study it in the following week.
In any particular week he studies not more than one of the subjects studied in the preceding week.
QUES62
Which of the following is a possible sequence of combinations for the student in the two successive weeks?
a.Week1: Philosophy, biology, economics. Week2: biology, mathematics, literature
b.Week1: philosophy, biology, mathematics. Week2: philosophy, biology, literature
c.Week1: philosophy, mathematics, literature. Week2: philosophy, biology, economics
d.Week1: biology, mathematics, literature. Week2: philosophy, economics, mathematics
Answer-c

Answer
63-a
64-a
QUES 65
If x,y,z are consecutive integers , and if x>y>z , which of the following must be a positive odd integer?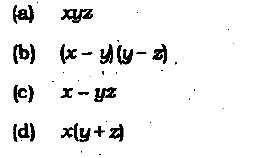

Answer-b
QUES 66
Suppose one wishes to prove that "if all X are Y, then all Z are W". To do this, it would suffice to show that: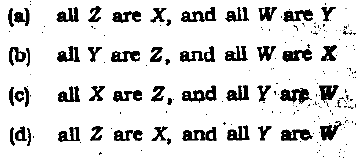

Answer-d
QUES 67
Let X & Y be statements. If we want to disprove the claim that "X implies Y", we need to show that: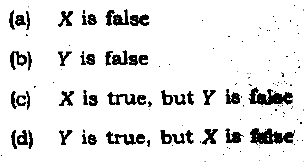

Answer-c

Answer-
QUES 70
Let P(n,m) be a property about two integers n & m. If we want to prove that "for every integer n, there exists an integer m such that P(n,m) is true", then we should do the following:
a.Let n & m be arbitrary integers. Then should that P(n,m) is true.
b.Find an integer m such that P(n,m) is true for every integer n.
c.Let n be an arbitrary integer. Then find an integer m possibly depending on such that P(n,m) is true.
d.Find an integer n and an an integer m such that P(n,m) is true.
Answer-c

[Arushi :))]

How to proceed with such questions 68,69?

[kangkan]

68.. X=> y means that if x is true,then y must be true..in this case y is false..therefore X cannot be true. Again\, Z=> X...but X is false..similiar logic will imply that z is fase...

i dont knw 69 :(

[bhavya jain]

Arushi, Kangan or anyone, do u have pdf of branson with you. If so, kindly mail me the copy to [e-mail]

[kangkan]

Sorry bhavya.. i am sticking to Abel and brenanke.

[Atika Gupta]

q69: answer d.

To show: X implies Y. Following are the ways:
1. Assume that X is true and then show that y is true. which is none of the options in the question.
2. You can prove it through contradiction. To arrive at contradiction we assume that X is true and Y is false. (Notice that this is nothing but the negation of  statement X implies Y that is, given X, Y is not true).
Once we do that we will arrive at a result which will contradict our assumption.Therefore, X implies Y.

option a is not correct as if we show X implies Z and Z implies Y , then it does not necessarily implies that X implies Y as we require the assumption of transitivity here.
option b clearly in no way show that X implies Y.
option c, is not a way to arrive at the contradiction. When X is false and Y is true then X implies Y is true but that does not lead to a contradiction.

[Arushi :))]

No bhavya..I don't have it. Sorry.

[ojaswini]

the answer to 69 is C as it is NOT a valid way. All others are valid.

On Mon, Mar 3, 2014 at 7:20 PM, Atika Gupta [via Discussion forum] <[hidden email]> wrote:

q69: answer d.

To show: X implies Y. Following are the ways:
1. Assume that X is true and then show that y is true. which is none of the options in the question.
2. You can prove it through contradiction. To arrive at contradiction we assume that X is true and Y is false. (Notice that this is nothing but the negation of  statement X implies Y that is, given X, Y is not true).
Once we do that we will arrive at a result which will contradict our assumption.Therefore, X implies Y.

option a is not correct as if we show X implies Z and Z implies Y , then it does not necessarily implies that X implies Y as we require the assumption of transitivity here.
option b clearly in no way show that X implies Y.
option c, is not a way to arrive at the contradiction. When X is false and Y is true then X implies Y is true but that does not lead to a contradiction.

---

If you reply to this email, your message will be added to the discussion below:

http://discussion-forum.2150183.n2.nabble.com/JNU-ECOM-2010-QUES-62-70-tp7585014p7585026.html

To start a new topic under General Discussions, email [hidden email]
To unsubscribe from Discussion forum, click here.
NAML

[Ridhika]

69 should be (b)

options a and d are difinitely valid ways to prove X=> Y.

(c) will actually prove that Y if and only if X. Which also proves the weaker condition that Y if X (ie. x=> Y).

[Ashima]

Using Truth Table:

X Y X implies Y
F T     T

Option c says let x be false, and y be true, this will imply x implies y. Now if i deduce a contradiction this wont be valid way to show x implies y.

Isn't it?

[Homer Simpson]

i think its (c)

if i assume that x is false and y is true, that means i believe p=> Q is true. now if i get a contradiction on that, how can i say my assumption is true??

[Ashima]

Yeah! So even if the assumptions are wrong that makes x true and y false, and again x implies y is false. Which again makes c! So c it is! Tsuki?

[Homer Simpson]

yeah its surely (c)