JNU ECOM 2010 ques 41-50

[Arushi :))]

Sorry guys. Due to some reason i couldnt post questions for the last two days. neways m back now
QUES41
Which of the following is a function?
a. A rule that assigns the circumference of a rectangle to its area.
b. A rule that assigns to each number its square root.
c. A rule that assigns to each person in a classroom his/her height.
d. A rule that assigns the salary of a person to his/her years of education.
Answer-c
QUES 42-45
Consider a country in which there are four different types of people Red, Blue, Green and yellow. All Reds earn the same income. The same is true about Blues, Greens & yellows. However, the Red income, the blue income, the green income & yellow income can be different from each other. A distribution of income of a country i given by Di specifies the Red income, Blue income, Green income & Yellow income & also the number of Reds, blues, Greens and yellows. the following table gives the possible income distribution for the country: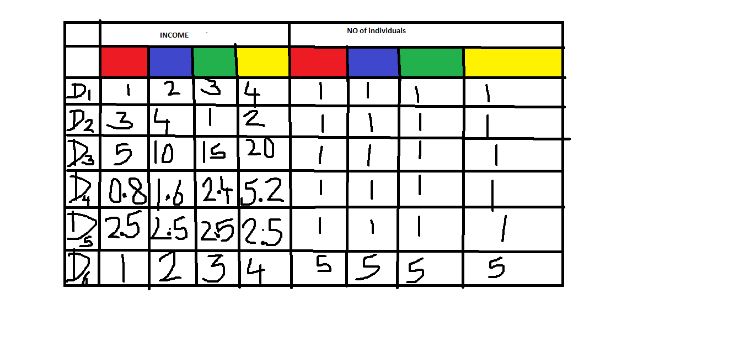

QUES 42
Let Gi denote the Ginni coefficient for the income distribution i. Which of the following is true?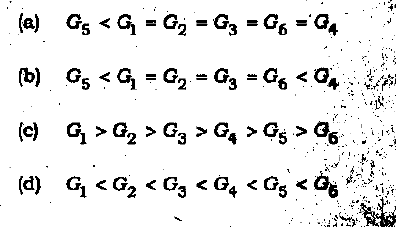

Aswer - b
QUES43
Let sigma i denote the standard deviation for the income distribution i. Which of the following is true?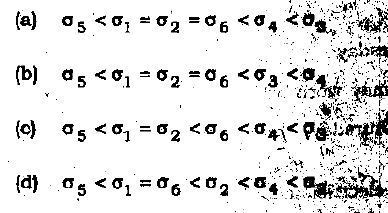

Answer- a

Answer 44- b

Answer-b
QUES 47
In case the painter works on Friday, which among the following statements must be untrue?
a. The carpenter may work on Wednesday.
b. The carpenter & electrician may work on consecutive days.
c. In case, the carpenter works on Thursday , the electrician has to work on the previous day, i.e Wednesday
d. The plumber may work before the electrician does.
Answer-c
QUES48
Which arrangement among the following is possible?
a.The painter will work on Wednesday & the plumber on Thursday.
b.The carpenter will work on Tuesday & the painter on Friday.
c.The painter will work on Monday & the carpenter on Thursday.
d.The carpenter will work on Wednesday & the plumber on Thursday.
Answer-d
QUES 49
There are two egg delivery boys you can order eggs from . The probability of the first boy falling & breaking all the eggs is 1/2 and the probability of second boy falling & breaking all the eggs is 1/5. How would you distribute your order for eggs so as to minimize expected loss of eggs?
a. Order all your eggs from the first boy.
b. Order all your eggs from the second boy.
c. Distribute the order for eggs between the two boys equally.
d. Order three-fourths of your eggs from first boy & the rest from the second boy.
Answer
QUES50
If you integrate the function f(x)=1/x from 1 to 3, you get:
a. 2
b. log3
c. log4
None of the above
Answer-b

[Arushi :))]

How to do 49?
And for 45 i think the answer is part a. No idea
please help with these two n confrm the rest

[kangkan]

Let the total no of eggs to be ordered be 100..let us give X to boy 1 and 100-x to boy 2

Let Y be the no of eggs we ultimately get

E(Y)= 0.5*x+0*x+ 0.8*(100-x)+0*(100-x)
E(y)= 80-0.3x

Now we will seek to maximize Y. It will be max if x=0.

So we will place the entire order on boy 2

[The Villain]

Hi Arushi

Could you explain me questions 42-25...

[Arushi :))]

Thanks kangkan..:)
hi ron
for these questions u should be having knowledge of ginni coefficient & measures of central tendency
For ques 42
for finding out ginni coefficient we have to take absolute deviation of incomes pairwise , i.e difference of each term with the other , add them up. and then we divide it by 2*mean income*n^2
example for D1
consider red people
deviation would be(absolute)
1-2 = 1,
1-3 = 2
1-4 = 3
then for blue people : 2-1=1 ,2-3=1, 2-4=2
then for green, 3-1=2 , 3-2=1, 3-4=1
then for yellow 4-1=3, 4-2=2, 4-3=1
next we have to add all these deviations and divide by 2n^2* mean income
mean income is 10/4=2.5
n^2= 16
n sum of deviations is 20
so ginni coeff would be 0.5
 the no. of people n incomes are same in country 2 .. thus G1= G2
then option c & d ruled out
only comparison between country 4 & 6 is left
coming to country 6
the sum of deviations is 20
but there are 5 people of each kind so we will multiply it by 5 = 100.
then mean income is 50/20= 2.5
and n^2= 400
so G6 would be 0.1
and lastly for country 4
calculating will give sum of deviations as 28
n^2 = 16
mean income = 2.5
G4= 0.7
G4>G6
Hence option b

[Arushi :))]

Ques 43
using the formula of standard deviation and taking each country as different distribution....
we get same std deviation for country 1 , 2, 6 =1.1
country 4 ' s standard deviation is 1.6 and country 3's standard deviation is 5.5
so ans would be part a..

[Arushi :))]

For ques 44..
the mean income for country 1, 5 ,6 2 is same 10/4 = 2.5
median is  5/2 for all of them = 2.5
for country 4 mean income is 2.5 and median is 2
so option c & d are ruled out..
for country 3 the median is 25/2 = 12.5
so country 4 has smallest median and country 6 has largest .. rest have the same
so option b

[Arushi :))]

45 i am not getting.
its not given whether people of a color can use an income of different color or not.
if they can use then , all of them are Pareto optimal because giving one's income to other would make one better off & other worse off.
But if you give blue income to yellow person and he can't use then he isn't made better off.so i dunno.someone help..

[The Villain]

Thank you Arushi :))Really appreciate

Please tell me Which book should i refer to for such questions and gini coefficient?

[Arushi :))]

hehe.. u are welcome ron
n u can refer to the book on development economics - debraj ray . this is the book we had in third year

[shietal]

Hi
Where can i get this question paper

[Arushi :))]

Hi shietal,
the question papers are available on this site itself on the Lessons page.

[Ridhika]

Arushi, I think the answer is (b) - all alocations are pareto optimal, because to move away from any of this given distributions you would have to take away some income (say z) of atleast 1 person (let that be an arbitary person i). Irrespective of who you give this z to, and whether or nnot they can use it, i will be made worse off. Therefore every allocation is pareto optimal.

[Anjali]

@Arushi , how have you calculated the median for this gini coefficient question ? Sum of middle incomes /2 ?
Don't we have to take their respective frequencies into account ?

[shietal]

IN THE FORMULA THAT YOU HAVE GIVEN, HAVE YOU DIVIDED THE NUMERATOR BY 2?